Das Übertragen und zeichnerische Ermitteln von Maßen und Winkeln ist meist genauer als das Messen. Aus diesem Grund haben die »Alten Meister« oft zu Zirkel und Schnur gegriffen, um das rechte Maß zu finden. In diesem Blogbeitrag möchten wir Ihnen gerne 10 Einsatzmöglichkeiten für den Zirkel vorstellen.
Vorweg: Manche Zirkel besitzen eine praktische Schnelleinstellung, die sich jedoch durch Druck auf die Zirkelschenkel leicht verstellt. Fassen Sie deshalb den Zirkel beim Zeichnen immer am Kopf an und üben Sie keinen Druck auf dessen Schenkel aus.
1. Maße anzeichnen und übertragen
Mit einem Zirkel können Sie wesentlich mehr machen als nur Kreise zeichnen. Auch zum Anreißen von regelmäßigen Maßen wie z. B. für Dübellöcher, Lochreihen für Bodenträger, Gürtellöcher ist ein Zirkel das beste Messwerkzeug. Auch zum Abgreifen und Übertragen von Maßen eignet er sich hervorragend (z. B. um einzelne Punkte aus einer maßstabsgetreuen Zeichnung aufs Werkstück zu übertragen). Mit einem Zirkel können Sie auch Maße von einem Werkstück abnehmen und prüfen, die sich mit einem Lineal oder Meterstab nur schwierig messen lassen.


2. Parallelen an geschwungenen Kanten anzeichnen
Um beispielsweise für Profil bzw. Hohlkehle bei Schildern, eine Saftrinne bei Schneidbrettern o. ä. parallel zur geschwungenen Kante anzuzeichnen, ist ein Zirkel wesentlich besser geeignet als ein Streichmaß. Je nach Komplexität der Form, kann man entweder einfach mit dem Zirkel am Rand entlangfahren/entlangstreichen und ihn dabei möglichst rechtwinklig zur Kante halten, oder Sie schlagen in regelmäßigen Abständen oder in Eckpunkten jeweils Kreisbögen und verbindet diese anschließend. Bei fest eingestelltem Zirkel ist die Markierung stets der maximale Abstand zum Rand. Sollten Sie einmal abweichen, orientieren Sie sich stets an der Innenkante der Linie. Der Zirkel kann nur nach außen abweichen, nicht nach innen.
3. Mittelpunkt einer Kreisfläche annähern
Das Ermitteln eines Mittelpunktes funktioniert nach dem gleichen Prinzip wie bei den geschwungenen Parallelen, nur dass diese möglichst nahe am vermuteten Mittelpunkt gezeichnet werden. Stellen Sie den Zirkel ungefähr auf den vermuteten Radius der Kreisfläche ein und schlagen Sie mehrere Zirkelbögen von unterschiedlichen Punkten an der Außenkante des Kreises. In der Mitte bleibt eine freie Fläche, die ungefähr dem Mittelpunkt des Kreises entspricht. Es spielt dabei keine Rolle, ob der Zirkel auf einen etwas größeren oder kleineren Radius als der tatsächliche Radius der Kreisfläche eingestellt ist. Diese Technik können Sie verwenden, um zum Beispiel bei einem Drechselrohling den Mittelpunkt zu finden oder eine Bohrung zum Aufhängen eines Holztellers zu platzieren.

Für die folgenden Zirkelkonstruktionen gilt: Zirkel zeichnen immer den Radius (r) an, d.h. wenn Durchmesser (D) gegeben ist, dann entspricht der Radius dem halben Durchmesser (r=D/2). Punkte werden wie folgt angegeben: Mittelpunkt = M, weitere Mittelpunkte = M1, M2 etc., Hilfspunkte = P bzw. P1, P2… und ermittelte (Schnitt-)Punkte = A, B, C… bzw. A1, B1 etc.
4. Strecke halbieren/90° Winkel ermitteln
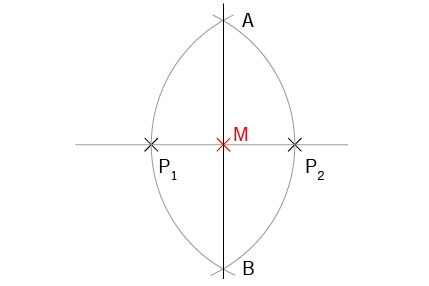
Um eine Strecke zwischen zwei Punkten exakt zu halbieren, gehen Sie wie folgt vor:
- Auf einer Linie (Basis) zwei Punkte definieren (P1, P2).
- Den Zirkel auf Radius P1-P2 oder größer einstellen.
- Ausgehend von den beiden Punkten jeweils einen Kreisboden oberhalb und unterhalb der Linie schlagen. Es entstehen zwei Schnittpunkte A und B.
- Die beiden Schnittpunkte A und B verbinden. Die so gezeichnete Linie schneidet die Basis genau in der Mitte zwischen P1-P2. Die Linie steht exakt rechtwinklig zur Basis (90°).
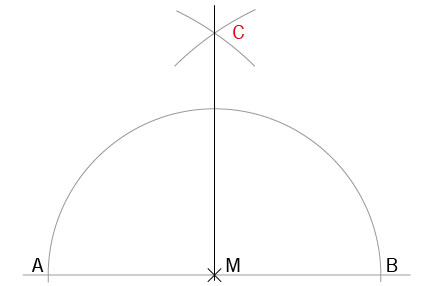
Auf ähnliche Weise lässt sich auch an einer Kante ein 90° Winkel zeichnen:
- Markieren Sie an der Kante den Punkt (M), in dem der »Rechte Winkel« stehen soll.
- Von Punkt M aus markieren Sie mit einem Kreisbogen an der Kante zwei Punkte A/B.
- Den Radius r vergrößern (ideal ist r = A-B) und von den Punkten A und B jeweils einen Kreisbogen oberhalb Punkt M schlagen, so dass Schnittpunkt C entsteht.
- Den Schnittpunkt C mit Punkt M verbinden. Die so gezeichnete Linie steht genau im Punkt M rechtwinklig zur Kante.
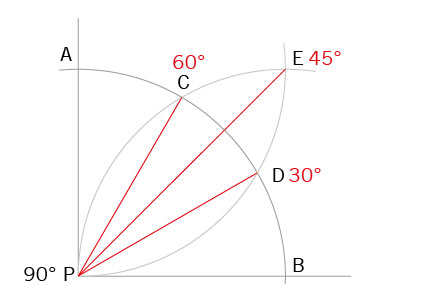
5. 30°/60° und 45° Winkel ermitteln
Um 30° und/oder 60°-Winkel anzureißen, wird zunächst wie oben ein 90° Winkel konstruiert.
- Aus Punkt P einen ¼-Kreisbogen über beide Schenkel (Senkrechte und Waagerechte) zeichnen und die Punkte A und B markieren.
- Mit dem gleichen Radius in A und B einstechen und zwei weitere Kreisbögen nach oben schlagen. Auf dem ersten Kreisbogen ergeben sich die Schnittpunkte C und D. Der Schnittpunkt der beiden neuen Kreisbögen ergibt Punkt E.
- C, D und E jeweils mit P verbinden. C-P = 60°, D-P = 30° und E-P = 45°
6. Winkel übertragen
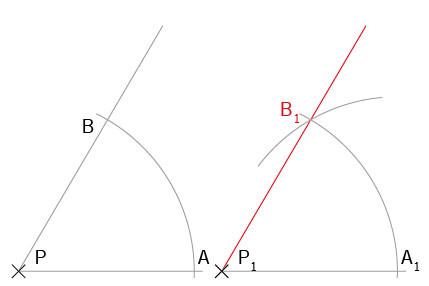
Wenn Sie einen bestimmten Winkel auf ein anderes Werkstück übertragen möchten, können Sie dies auch ohne Schmiege oder Winkelmesser tun. Dazu folgende Methode anwenden:
- Um den Scheitelpunkt P einen Kreisbogen schlagen, das ergibt an den Schenkeln die Punkte A und B.
- Die Einstellung des Radius beibehalten, im Ausgangspunkt des neuen Winkels P1 einstechen und einen Kreisbogen schlagen. Es entsteht A1.
- Nun die Strecke A-B in den Zirkel nehmen und damit in A1 einstechen und so B1 anzeichnen.
- B1 mit P1 verbinden. Die so gezeichnete Linie steht im gleichen Winkel wie die Ausgangslinie.
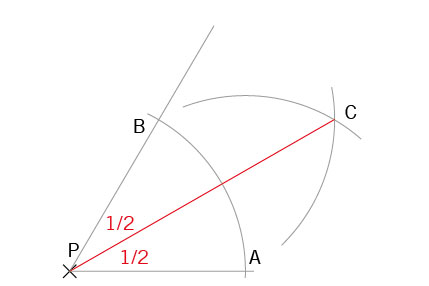
7. Winkel halbieren (Gehrungswinkel ermitteln)
Auch einen Gehrungswinkel können Sie mit Zirkel, Lineal und Stift genau ermitteln. Das Prinzip ist das gleiche wie beim Halbieren einer Strecke, nur dass die Strecke einen »Knick« hat.
- Um den Scheitelpunkt P einen Kreisbogen über beide Schenkel schlagen. Schnittpunkte A und B entstehen.
- Jeweils in A und B einstechen und mit zwei Kreisbögen den Schnittpunkt C anreißen.
- Schnittpunkt C mit P verbinden, dies ergibt die Winkelhalbierende.
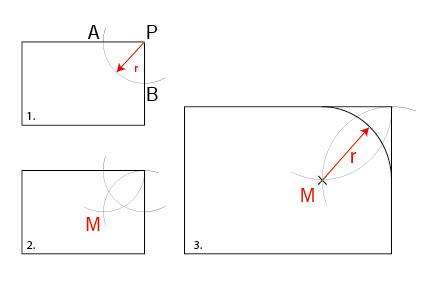
8. Eckenrundung anreißen
Normalerweise wird ein runder Gegenstand wie einen Teller oder eine Dose genommen, um damit in Ecken eine Rundung anzuzeichnen. Wenn Sie jedoch einen exakten Radius haben möchte, gehen sie folgendermaßen vor:
- Den gewünschten Radius r einstellen und von der Ecke aus zwei Markierung A und B an den Kanten abtragen.
- Mit unverändertem Radius von A und B aus zwei Zirkelschläge in der Nähe des vermuteten Mittelpunktes des Eckradius schlagen. Deren Schnittpunkt ergibt den genauen Mittelpunkt der Eckrundung M.
- Nun in M den Zirkel einstechen und den Eckradius r anzeichnen.
9. Größtmögliches Sechseck anreißen
Auf die folgende Art kann das größtmögliche Sechseck auf einem Brett angezeichnet werden:
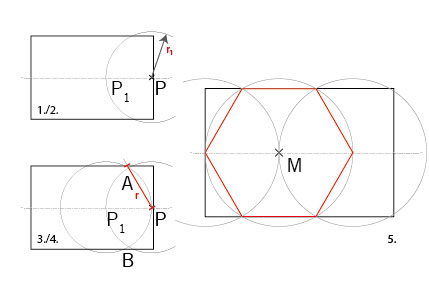
- Waagerechte Mittellinie anzeichnen.
- Einen Kreisbogen mit einem etwas größeren Durchmesser als die Höhe des Brettes schlagen (D = 2r1). Der Ausgangspunkt P ist auf der Mittellinie nahe der Kante (an der Kante kann der Zirkel nicht gut eingestochen werden). Am Schnittpunkt von Kreisbogen und Mittellinie ergibt sich Punkt P1.
- Von P1 mit unverändertem Radius einen Kreisbogen zeichnen. Es ergeben sich die Schnittpunkte A und B.
- Punkte A (oder B) mit P verbinden und die Linie zur Kante hin verlängern.
- Die so ermittelte Strecke P-Kante ist der gesuchte Radius r für das größtmögliche Sechseck. Damit kann nun das Sechseck wie gewohnt angezeichnet werden.
10. Harmonisches Oval konstruieren
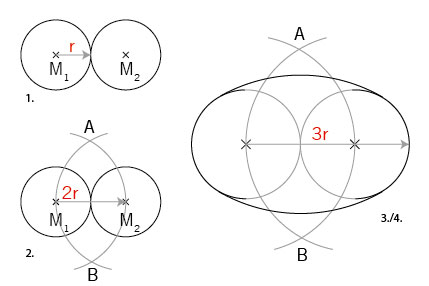
Auf die folgende Art kann ein harmonisches Oval angezeichnet werden:
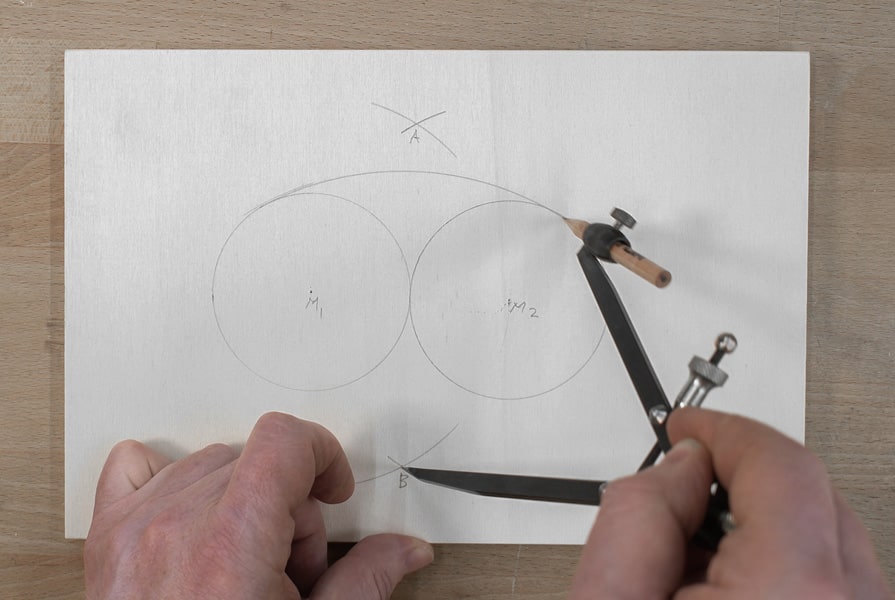
- Zeichnen Sie zwei Kreise nebeneinander (r = ¼ Länge des Ovals), die sich tangieren.
- Den Zirkel nun auf den Durchmesser (r2 = 2r) einstellen (Strecke zwischen den beiden Mittelpunkten M1-M2). Damit zwei Kreisbögen schlagen. Die Schnittpunkte A und B ergeben sich.
- Den Zirkel in M1 belassen und von dort den Außenradius des anderen Kreises abnehmen (r3 = 3r).
- Nun jeweils in A und B einstechen und mit zwei Bögen das Oval schließen.
Auf gleiche Weise wird ein einfacher Korbbogen, also ein halbes Oval, konstruiert.
Mit dem Zirkel lassen sich noch weitere geometrische Objekte wie z. B. ein Karniesbogen, eine Spirale oder Ellipsen konstruieren. Deren Konstruktion ist jedoch etwas aufwendiger und es gibt beispielsweise zum Anzeichnen von Ellipsen bessere Lösungen als den Zirkel, sodass wir dazu voraussichtlich eigene Beiträge machen werden.